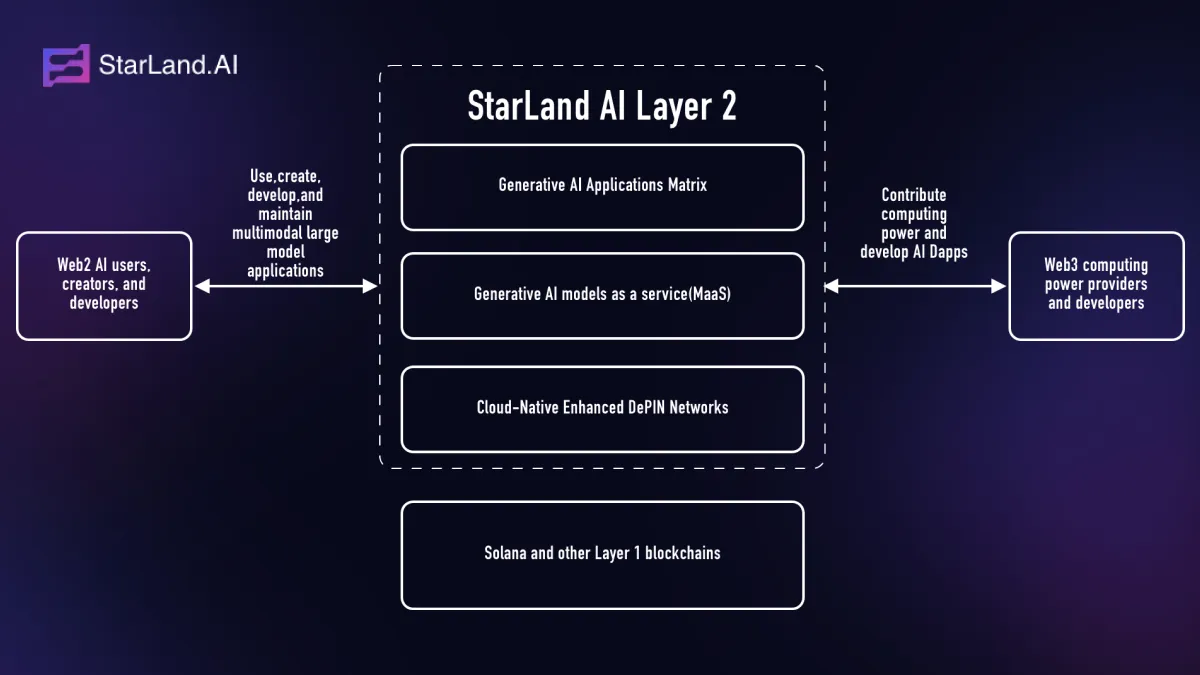
The Core of StarLandAI’s DePIN:Proof of Computation

What are Verifiable Computing and Proof of Computation?
Verifiable Computing is a computational paradigm that allows computers to delegate the computation of specific functions to other untrusted clients while ensuring that the results obtained can be effectively verified. These clients, upon completing the relevant computations, provide proof that confirms the correctness of the computation process. With the significant advancement of decentralized computing and cloud computing, the scenario of outsourcing computational tasks to untrusted parties has become increasingly common. It also reflects a growing demand for enabling devices with limited computational power to delegate their computational tasks to third-party, more powerful computational service platforms. The concept of verifiable computing was first proposed by Babai et al. [1] and has been explored under various names, such as “checking computations” (Babai et al.), “delegating computations” [2], “certified computation” [3], etc. The term “verifiable computing” was explicitly defined by Rosario Gennaro, Craig Gentry, and Bryan Parno [4].
Proof of Computation (PoC) is a cryptographic protocol that allows a verifier to confirm that a computational task has been correctly executed without having to re-execute the entire computation process. The core idea of this protocol is that the executor of the computation task provides a brief proof, which is compact enough to be efficiently verified while also conclusively demonstrating the correctness of the computation. In PoC, the executor first computes the input data and generates an output result. Then, they create a proof that contains sufficient information to verify the correctness of the output result without revealing the input data or the specifics of the computation. The verifier can use this proof to confirm the correctness of the computation without knowing the specific computation process or the original data. Proof of Computation has applications in multiple fields, such as:
-
Cloud Computing: In cloud services, customers may wish to verify that their data is being processed correctly without disclosing the data itself. PoC allows cloud service providers to provide proof that they have correctly executed the computation task.
-
Distributed Systems: In a distributed computing environment, nodes may need to verify the computational results of other nodes to ensure the consistency and reliability of the entire system.
-
Blockchain: In blockchain technology, PoC can be used to verify the execution results of smart contracts, which is crucial for ensuring the security and transparency of decentralized applications.
-
Privacy Protection: PoC can be used to protect personal privacy as it allows the verification of the correctness of computations without disclosing the original data.
Verifiable Computing is a broad field that encompasses a variety of technologies and applications, and Proof of Computation (PoC) is a key technology within this field, used to achieve the verifiability of computations. PoC is a component of verifiable computing, and together they support a more secure and trustworthy computing environment.
Mainstream Proof of Computation Principles and Technologies
2.1 Proof of Computation (PoC) based on Zero-Knowledge Proofs
(1) Proof of Computation (PoC) based on Zero-Knowledge Proofs is a cryptographic method that allows a prover to demonstrate to a verifier that a computational task has been correctly executed without revealing the specifics of the computation or any sensitive data. The core advantage of this method lies in privacy protection and enhanced security, as the verifier only needs to know whether the result is correct, not how it was achieved. The main technical process is as follows:
-
Define the computational task: First, it is necessary to clarify what the computational task to be verified is. This could be a mathematical function, an algorithm, or any other type of computational process.
-
Generate the proof: The prover performs the computational task and generates a zero-knowledge proof. This proof is a cryptographic structure that contains sufficient information to prove the correctness of the computation without including any sensitive information about the computational inputs or intermediate steps. Zero-knowledge proofs typically rely on complex cryptographic constructs such as elliptic curves, pairings, or zero-knowledge SNARKs (Succinct Non-Interactive Arguments of Knowledge).
-
Verify the proof: Upon receiving the proof, the verifier runs a verification algorithm to check the validity of the proof. If the proof is valid, the verifier can be confident that the computational task has been correctly executed without knowing the specific computational details.
-
Maintain privacy: Throughout the process, the prover does not need to disclose any information about the computational inputs. This is crucial for protecting data privacy and preventing potential data leaks.
(2) There are various technical approaches to implementing PoC based on zero-knowledge proofs, including:
-
zk-SNARKs: This is a special type of zero-knowledge proof that provides properties of succinctness, non-interaction, and knowledge of proof. zk-SNARKs allow the prover to generate a short proof that the verifier can verify offline without interacting with the prover.
-
zk-STARKs: This is a zero-knowledge proof that does not require a trusted setup, offering transparency and scalability. Compared to zk-SNARKs, zk-STARKs do not rely on complex mathematical puzzles, making them easier to implement and verify.
-
Bulletproofs: This is a new type of zero-knowledge proof that provides efficient verification while protecting privacy, particularly suitable for blockchain applications involving transaction amounts.
2.2 Proof of Computation based on Trusted Hardware
(1) In contrast to the purely software implementation of zero-knowledge proofs, we can also implement PoC based on Trusted Hardware, which is a method that utilizes physical security features to ensure the correctness and security of the computation process. The implementation typically involves hardware security modules (such as secure processors, cryptographic cards, or Trusted Execution Environments TEE), designed to provide an isolated and secure execution environment, resistant to external attacks and unauthorized access. The main technical process is as follows:
-
Build secure boot for hardware and applications: Secure boot is a process that ensures only authenticated, unmodified software can be executed on the hardware. This is a fundamental step in ensuring hardware security.
-
Agree on cryptographic anchoring: When using trusted hardware, computational proofs are often combined with cryptographic anchoring. This means that the results or evidence of computation are associated with a cryptographic key, which is protected by trusted hardware.
-
Compute based on Trusted Execution Environment (TEE): TEE is a combination of hardware and software that provides a secure execution environment, protecting the code and data loaded into the TEE from external attacks and tampering. TEE typically includes a secure processor and an isolated memory area.
-
Verify computation through remote attestation: Remote attestation is a mechanism that allows the authenticity and integrity of the TEE to be verified remotely. Through remote attestation, a client can be assured that it is interacting with a genuine, unmodified TEE.
(2) The advantage of PoC based on trusted hardware lies in their provision of a physically secure computing environment, which is theoretically very difficult to breach. They also offer high performance.

StarLandAI’s proof of computation
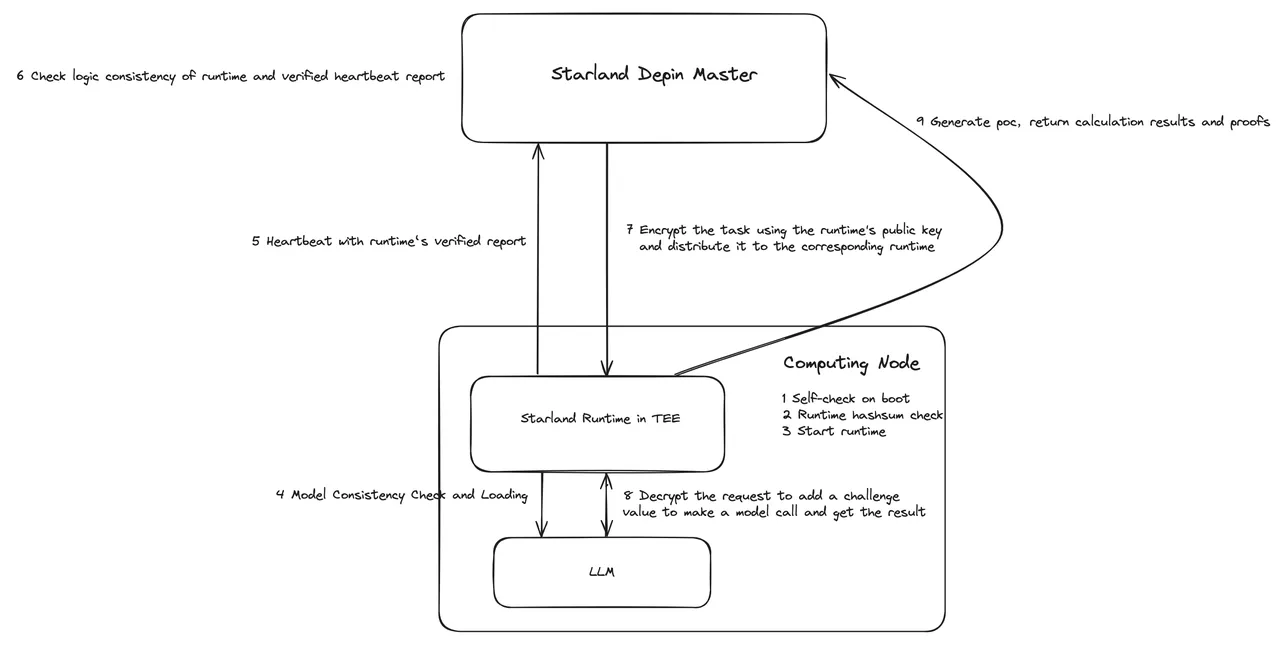
3.1 Overall Process
To provide a reliable and scalable computational power infrastructure, StarLandAI has implemented a complete set of hardware authentication and proof of computation mechanisms by combining secure hardware with cryptographic algorithms. The overall process is illustrated in the figure below:
-
During the startup phase of the computational node, a self-check of the device is performed to inspect the status of components such as the GPU and CPU, as well as the versions of their drivers.
-
The computational node daemon verifies the hash of the StarLand runtime image.
-
The computational node daemon launches the StarLandAI runtime. If a trusted execution environment (TEE) is available, it will initiate the runtime based on the TEE.
-
The StarLandAI runtime conducts a consistency check and loads the model.
-
Once launched, the StarLandAI runtime checks its own operating environment, loads the model, identifies the certificate and device information, generates a runtime authentication report, and sends it to the StarLandAI DePIN Master in the form of a heartbeat.
-
The StarLandAI DePIN Master validates the runtime information based on the received report and completes the node access procedure.
-
For a computational power assessment and inference task, the StarLandAI DePIN Master encrypts the task parameters and challenge values using the public key of the runtime and issues them.
-
The runtime decrypts the task information to generate a runtime challenge response and a model-specific call challenge value, then calls the model to obtain the inference result.
-
The runtime verifies the model challenge response value and the inference result. It constructs a single-call computational proof using the runtime challenge response generated in step 8 and returns it to the StarLandAI DePIN Master. Upon receiving the response, the StarLandAI DePIN Master completes the check and results, concluding the entire process.
3.2 Composition of Computation Proof
StarLandAI’s algorithm for generating computation proofs is an innovative solution designed to optimize the utilization of computational resources. The algorithm not only intelligently evaluates the computational capacity of each computational node to ensure the most suitable computational tasks are matched, but it also takes into account the computational throughput of the nodes to maximize efficiency and performance. Moreover, what sets StarLandAI apart is its in-depth analysis of the model capabilities supported by the nodes, allowing us to accurately schedule complex computational tasks, especially those advanced applications that require specific model support. With this comprehensive consideration, StarLandAI can significantly enhance the execution speed and accuracy of computational tasks while reducing operational costs. Our computation proof generation algorithm is the core that drives efficient, intelligent, and scalable management of computational resources, providing unparalleled support for AI and machine learning workloads. StarLandAI is committed to leading the future of computational resource management through cutting-edge technology, unlocking infinite possibilities. StarLandAI computation proofs are divided into two categories:
- Runtime Verified Report: A periodic assessment proof for an integrated computational node.
- Proof of Inference Computation: A workload assessment proof for a specific inference task.
(1) Runtime verified report
The Runtime Verified Report is a periodic assessment proof for an integrated computational node. After the node completes self-inspection and initialization, it will periodically report its heartbeat, which must include the Runtime Verified Report. The specific structure of the Runtime Verified Report includes the following content:
- Node Identity Address (associated with the identity certificate)
- Node Computational Power Score (the calculation formula will be provided later)
- Node Computational Power Equipment Information
- Node Geographic Distribution Information
- Node Identity Authentication Signature
- Hardware Authentication Report of the Runtime
The node identity corresponds to a pair of public and private keys. StarLandAI will receive the node-related registration identity certificate information to support the verification, encryption, and authentication of the subsequent computational process. At the same time, the computational power equipment information, computational power score, and geographic distribution information will support StarLandAI in selecting the optimal computational power for scheduling during subsequent inference tasks. Each heartbeat report requires a node identity authentication signature to prevent impersonation by malicious parties.
(2) Proof of inference computation
Proof of Inference Computation is a proof of computational contribution for a specific inference task, which specifically includes the following content:
- Computational Node Information
- Hardware Authentication Report of the Computational Runtime
- Task Challenge Response Value and Signature
- Hash of the Model Snapshot Corresponding to the Task
- Node Computational Power Score Involved in This Task
Appendix
Computation Power Score = S(Computing_Card_Count×Single_Card_Inference_Throughput×Deployed_Model_Scale×Model_Count) Where:
- ScoreScore: Represents the final score or performance metric.
- S: Is a function that normalizes the product of several factors into a standardized score.
- Computing_Card_CountComputing_Card_Count: Indicates the number of computing devices (such as GPUs or TPUs).
- Single_Card_Inference_ThroughputSingle_Card_Inference_Throughput: Refers to the ability of a single computing device to process model inferences within a unit of time.
- Deployed_Model_ScaleDeployed_Model_Scale: Represents the measure of the scale or complexity of the deployed model, which correlate with the number of model parameters or computational requirements.
- Model_CountModel_Count: Denotes the total number of models deployed in the computational environment.
Reference
-
Babai, László; Fortnow, Lance; Levin, Leonid A.; Szegedy, Mario (1991–01–01). “Checking computations in polylogarithmic time”. Proceedings of the twenty-third annual ACM symposium on Theory of computing — STOC ’91. STOC ’91. New York, NY, US: ACM. pp. 21–32. CiteSeerX. 10.1.1.42.5832. doi: 10.1145/103418.103428. ISBN 978–0897913973. S2CID 16965640.
-
^ Goldwasser, Kalai, Yael Tauman; Rothblum, Guy N. (2008–01–01). “Delegating computation”. Proceedings of the fortieth annual ACM symposium on Theory of computing. STOC ’08. New York, NY, US: ACM. pp. doi: 10.1145/1374376.1374396. ISBN 9781605580470. S2CID 47106603.
-
^ Jump up to:(a) (b) “Computationally Sound Proofs”. SIAM Journal on Computing. 30 (4): 1253–1298. CiteSeerX 10.1.1.207.8277. doi: 10.1137/S0097539795284959. ISSN
-
Gennaro, Rosario; Gentry, Craig; Parno, Bryan (31 August 2010). Non-Interactive Verifiable Computing: Outsourcing Computation to Untrusted Workers. CRYPTO 2010. doi: 10.1007/978–3–642–14623–7_25.